largecats' blog data engineer

Variances in Type Systems

2020-12-01
work

The concept of variance is used to describe relations among subtyping. Subtyping is a relation defined between two types S and T, such that if S is a subtype of T (S <: T), then a thing of type S can be used in any context where a thing of type T is expected. E.g., if Cat is a subtype of Animal, a Cat can replace an Animal.

But how should the following be related?

  • Collection[Cat] vs Collection[Animal]
  • get_cat: () -> Cat vs get_animal: () -> Animal
  • print_cat: Cat -> () vs print_animal: Animal -> ()

This is where variance comes in. Variance refers to how subtyping of a more complex type relates to subtyping of its component type.

Variances

There are three major kinds of variances.

  • Covariance
  • Contravariance
  • Invariance

Covariance

Definition. A complex type is covariant in its component type if it preserves the subtyping of its component type.

E.g., in Scala, we can make the class Wrapper covariant in its type parameter T by adding a plus sign in front.

class Wrapper[+T] // Wrapper is covariant in T

In this case, if S <: T, then Wrapper[S] <: Wrapper[T].

Contravariance

Definition. A complex type is contravariant in its component type if it reverses the subtyping of its component type.

We can make Wrapper contravariant in its type parameter T by adding a minus sign in front.

class Wrapper[-T] // Wrapper is contravariant in T

In this case, if S <: T, then Wrapper[S] >: Wrapper[T].

Invariance

Definition. A complex type is invariant in its component type if its subtyping is not related to that of its component type.

We can make Wrapper invariant in T by not adding any annotation to the type parameter.

class Wrapper[T]  // Wrapper is invariant in T

In this case, if S <: T, then neither Wrapper[S] <: Wrapper[T] nor Wrapper[S] >: Wrapper[T]. Wrapper[S] and Wrapper[T] are simply not related in terms of subtyping.

Variances of Different Types

There are several types whose variances are worth examining.

Variances of Collection Types

Collection tyes refer to types like Array, List, etc.

Consider this question: If Cat is a subtype of Animal, how should Collection[Cat] relate to Collection[Animal]?

We can make Collection covariant, contravariant, and invariant. But the choice comes with trade-offs.

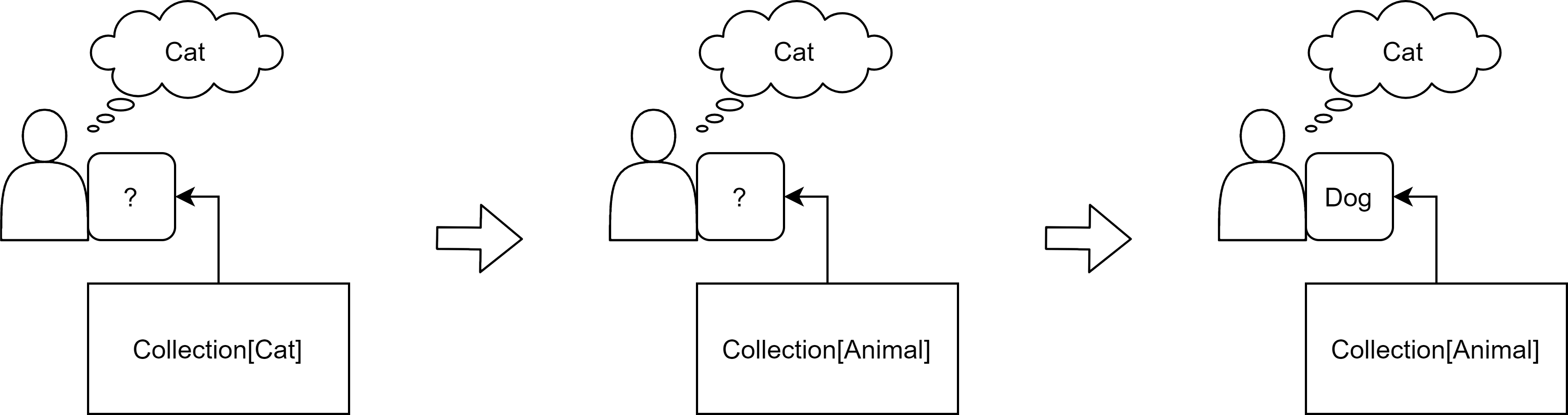
  1. Covariance is not safe for writing.
    Writing to covariant Collection.

    Suppose Collection is covariant, and suppose someone is writing to a Collection[Animal]. By covariance, Collection[Cat] <: Collection[Animal]. By definition of covariance, Collection[Animal] can be replaced by Collection[Cat]. But the writer might be writing a Dog type. It’s valid to write Dog to Collection[Animal] but not to Collection[Cat]. So we have a type mismatch.

  2. Contravariance is not safe for reading.
    Reading from contravariant Collection.

    Suppose Collection is contravariant, and suppose someone is reading from a Collection[Cat]. By contravariance, Collection[Animal] <: Collection[Cat]. By definition of contravariance, Collection[Cat] can be replaced by Collection[Animal]. But Collection[Animal] might contain Dog type, while the reader only expects to read a Cat. So again we have a type mismatch.

In general:

Safe? Read Write
Covariance Y N
Contravariance N Y
Invariance Y Y

“Safe” here means that the type system is strict enough to detect these type errors at compile time. However, a programming language may choose an “unsafe” rule and make up for it by implementing additional checks at run time. Here are some concrete examples:

  • Scala List is immutable, so we can read from it but not write to it via assignment. So it’s safe to make it covariant (indeed: It is defined as List[+A], see here).
  • Scala Array is mutable, so we can read from it and also write to it via assignment, so it should be invariant (indeed: It is defined as Array[T], see here).
  • Java Array is mutable and covariant, so it uses additional run time type checks to ensure type safety by checking for type errors every time a item is written to it.

Variances of Function Return Types

Consider this question: If Cat is a subtype of Animal, how is get_cat: () -> Cat related to get_animal: () -> Animal?

Arguing from intuition: if a function that returns an Animal is expected, we can always use a function that returns a Cat instead, because a Cat is an Animal. So get_cat <: get_animal.

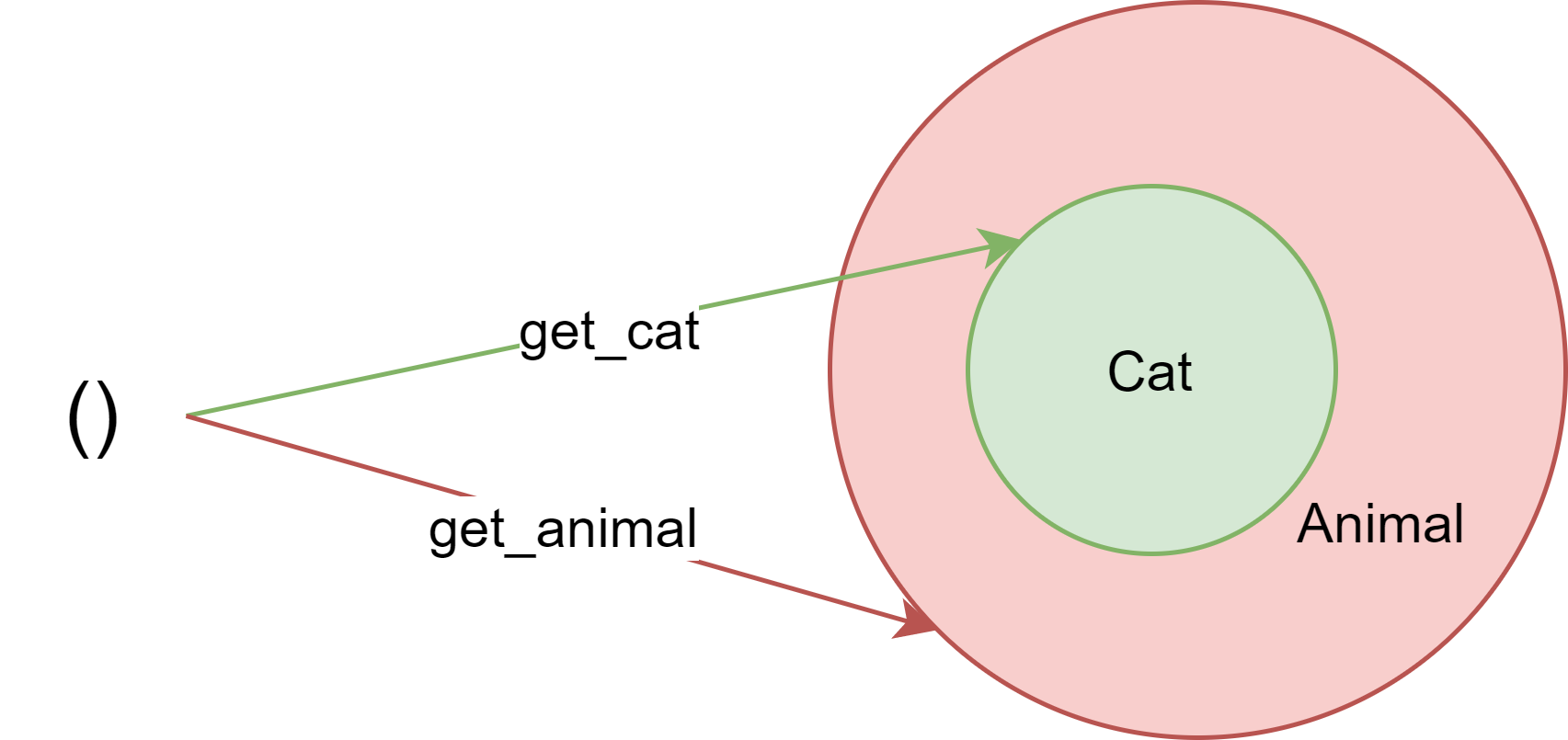
Arguing from definition: Since Cat can be used in any context where Animal is expected, get_cat can be used in any context where get_animal is expected, so get_cat <: get_animal.

In general, function is covariant in return type.

Variances of Function Parameter Types

Consider this question: If Cat is a subtype of Animal, how is print_cat: Cat -> () related to print_animal: Animal -> ()?

Arguing from intuition: If a function that accepts a Cat is expected, we can always use a function that accepts an Animal instead, because a Cat is an Animal. So print_aniaml <: print_cat.

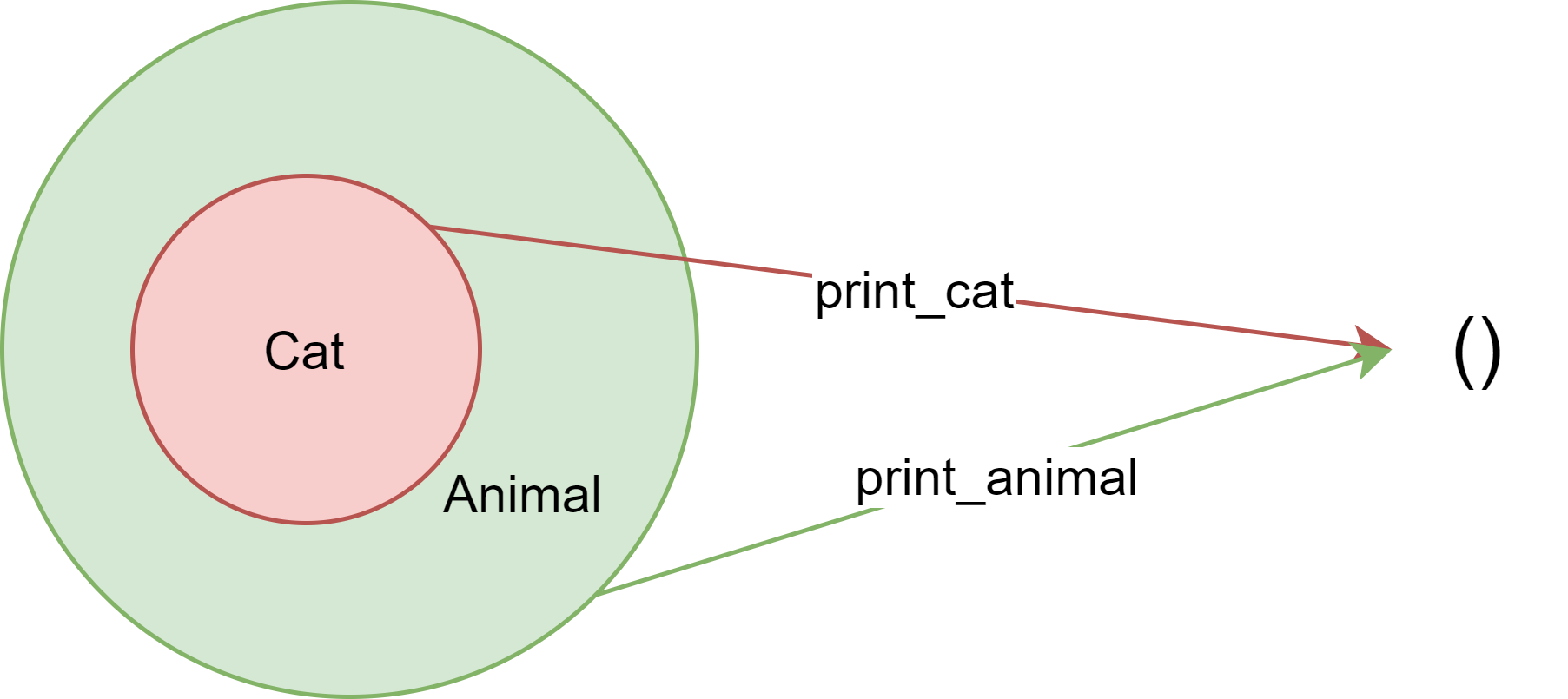
Arguing from definition: Since print_animal expects Animal as parameter and Cat can be used in any context where Animal is expected, print_animal must also be able to accept a Cat. So print_animal can be used where print_cat is expected. So print_animal <: print_cat.

In general, function is contravariant in parameter type.

Variances of Function Types

Consider this question: If Cat is a subtype of Animal, how are functions Cat -> Cat, Cat -> Animal, Animal -> Cat, and Animal -> Animal related?

Variances of function types follow from variances of function return types and parameter types.

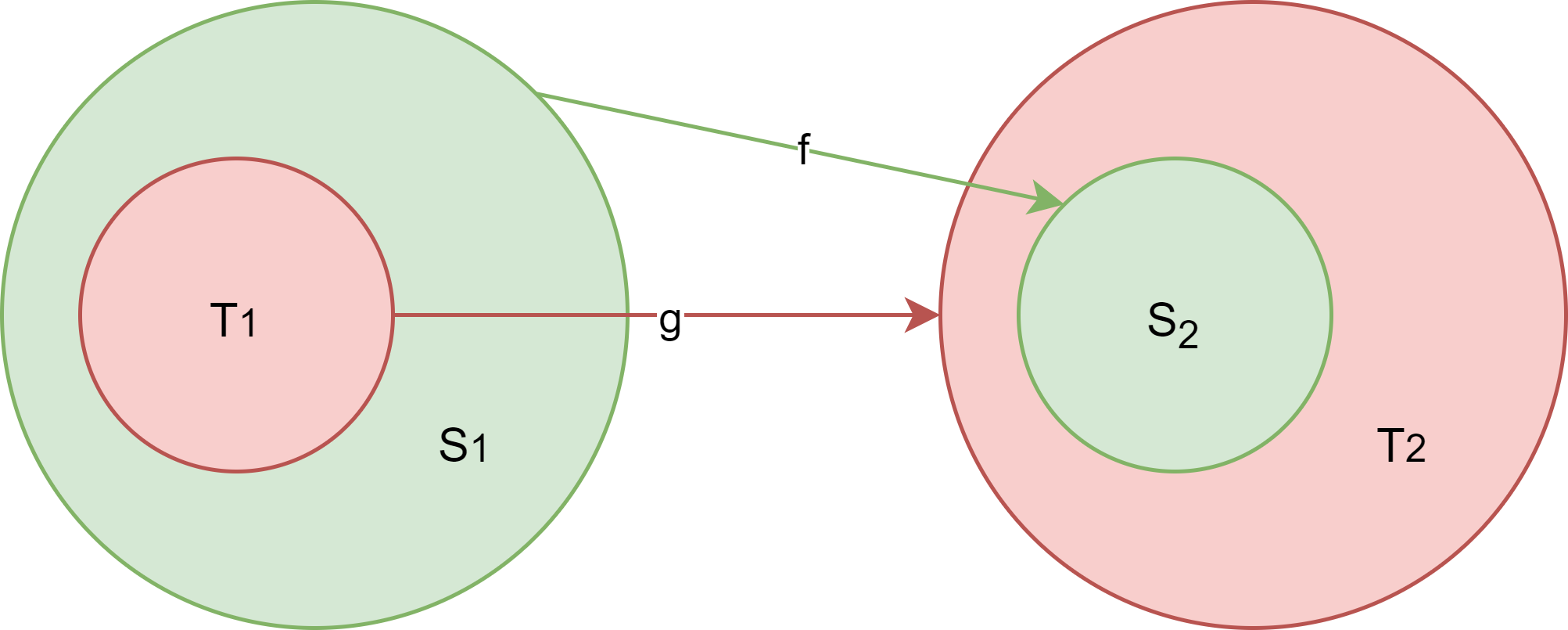
Animal -> Cat <: Cat -> Cat <: Cat -> Animal

The first relation is true because functions are contravariant in parameter type, and the second relation is true because functions are covariant in return type. Similarly,

Animal -> Cat <: Animal -> Animal <: Cat -> Animal

In general: \(f: S_1 \rightarrow S_2 \leq g: T_1 \rightarrow T_2 \text{ if } T_1 \leq S_1 \text{ and } S_2 \leq T_2.\)

Application

But why would anyone want covariance/contravariance? To ensure type-safety, we could have stuck to invariance all the time.

Turns out that there’s a trade-off between safety and flexibility. The pros for having covariance and contravariance is that more programs will be accepted as well-typed. On the other hand, it is harder to ensure type-safety while maintaining such flexibility.

Here’s a small application to show how covariance/contravariance is useful.

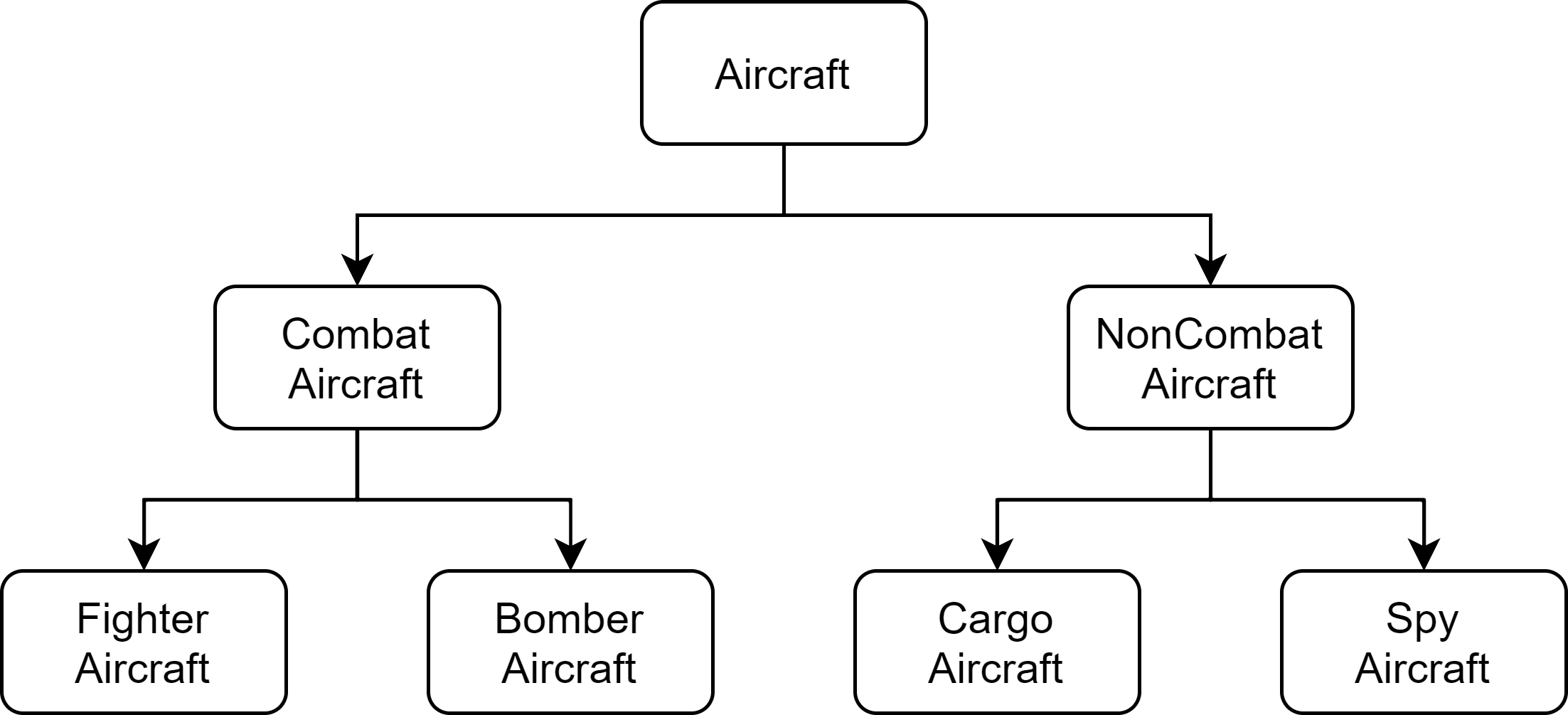
Component Type: Aircraft

We define a component type Aircraft.

trait Aircraft {
  val name: String
}

Classes CombatAircraft and NonCombatAircraft that inherit from Aircraft:

class CombatAircraft(val name: String) extends Aircraft
class NonCombatAircraft(val name: String) extends Aircraft

And classes FighterAircraft, BomberAircraft, CargoAircraft, and SpyAircraft that inherit from CombatAircraft and NonCombatAircraft, respectively:

class FighterAircraft(override val name: String) extends CombatAircraft(name)
class BomberAircraft(override val name: String) extends CombatAircraft(name)

class CargoAircraft(override val name: String) extends NonCombatAircraft(name)
class SpyAircraft(override val name: String) extends NonCombatAircraft(name)
Subtyping of Aircraft.

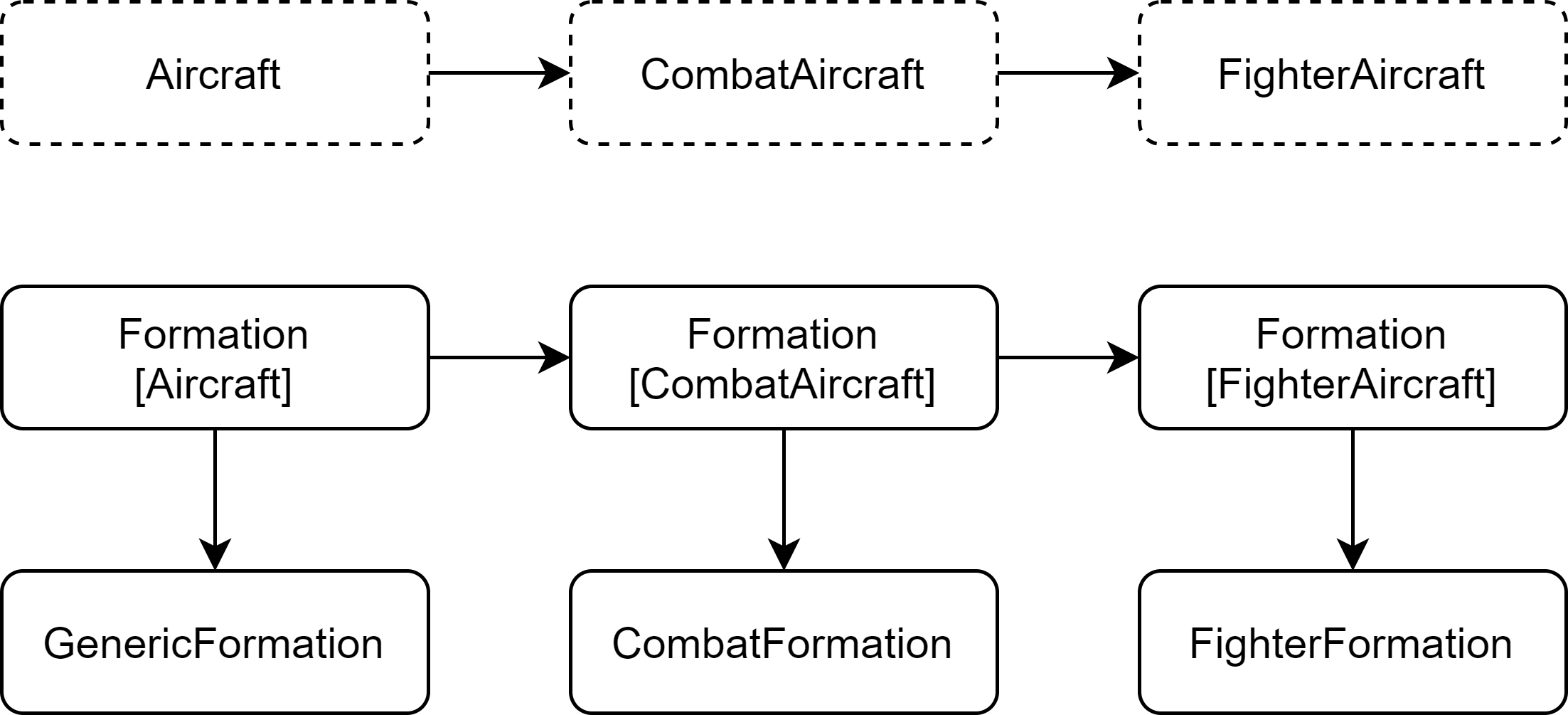
Covariant Type: Formation

We define a covariant type Formation to describe formations of aircrafts.

trait Formation[+A] { // covariant in A
  val leader: A
  val wingman: A
}

We then define GenericFormation, CombatFormation, FighterFormation that contain any Aircraft, CombatAircraft, and FighterAircraft, respectively.

class GenericFormation(val leader: Aircraft, val wingman: Aircraft) extends Formation[Aircraft]
class CombatFormation(val leader: CombatAircraft, val wingman: CombatAircraft) extends Formation[CombatAircraft]
class FighterFormation(val leader: FighterAircraft, val wingman: FighterAircraft) extends Formation[FighterAircraft]
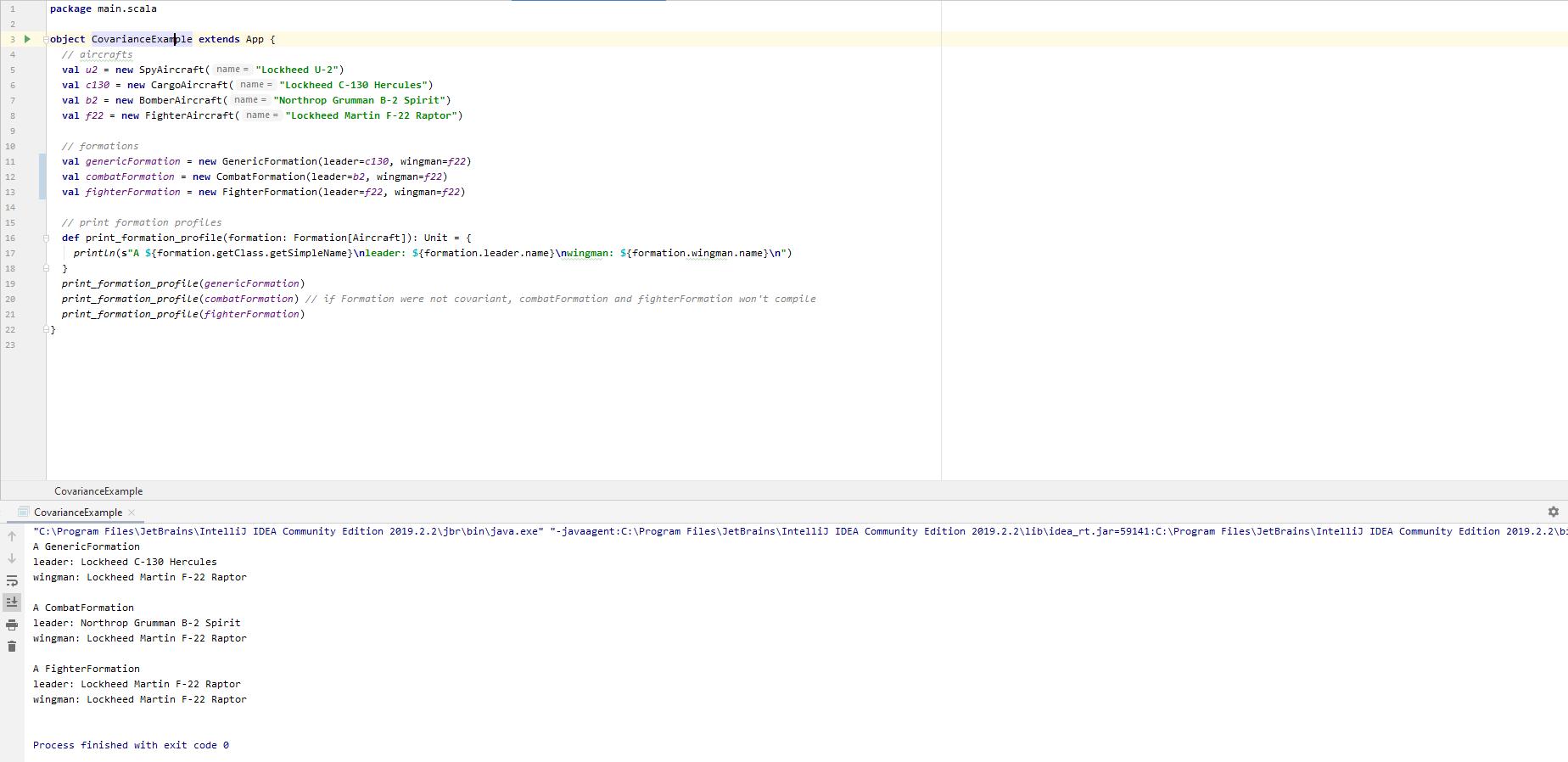
Formation is covariant in Aircraft and it preserves the subtyping of Aircraft.

We define aircrafts, formations, and a function print_formation_profile to print information about the leader and wingman in the formation. print_formation_profile accepts a paramter of type Formation[Aircraft].

object CovarianceExample extends App {
  // aircrafts
  val u2 = new SpyAircraft("Lockheed U-2")
  val c130 = new CargoAircraft("Lockheed C-130 Hercules")
  val b2 = new BomberAircraft("Northrop Grumman B-2 Spirit")
  val f22 = new FighterAircraft("Lockheed Martin F-22 Raptor")

  // formations
  val genericFormation = new GenericFormation(leader=c130, wingman=f22)
  val combatFormation = new CombatFormation(leader=b2, wingman=f22)
  val fighterFormation = new FighterFormation(leader=f22, wingman=f22)

  // print formation profiles
  def print_formation_profile(formation: Formation[Aircraft]): Unit = {
    println(s"A ${formation.getClass.getSimpleName}\nleader: ${formation.leader.name}\nwingman: ${formation.wingman.name}\n")
  }
  print_formation_profile(genericFormation)
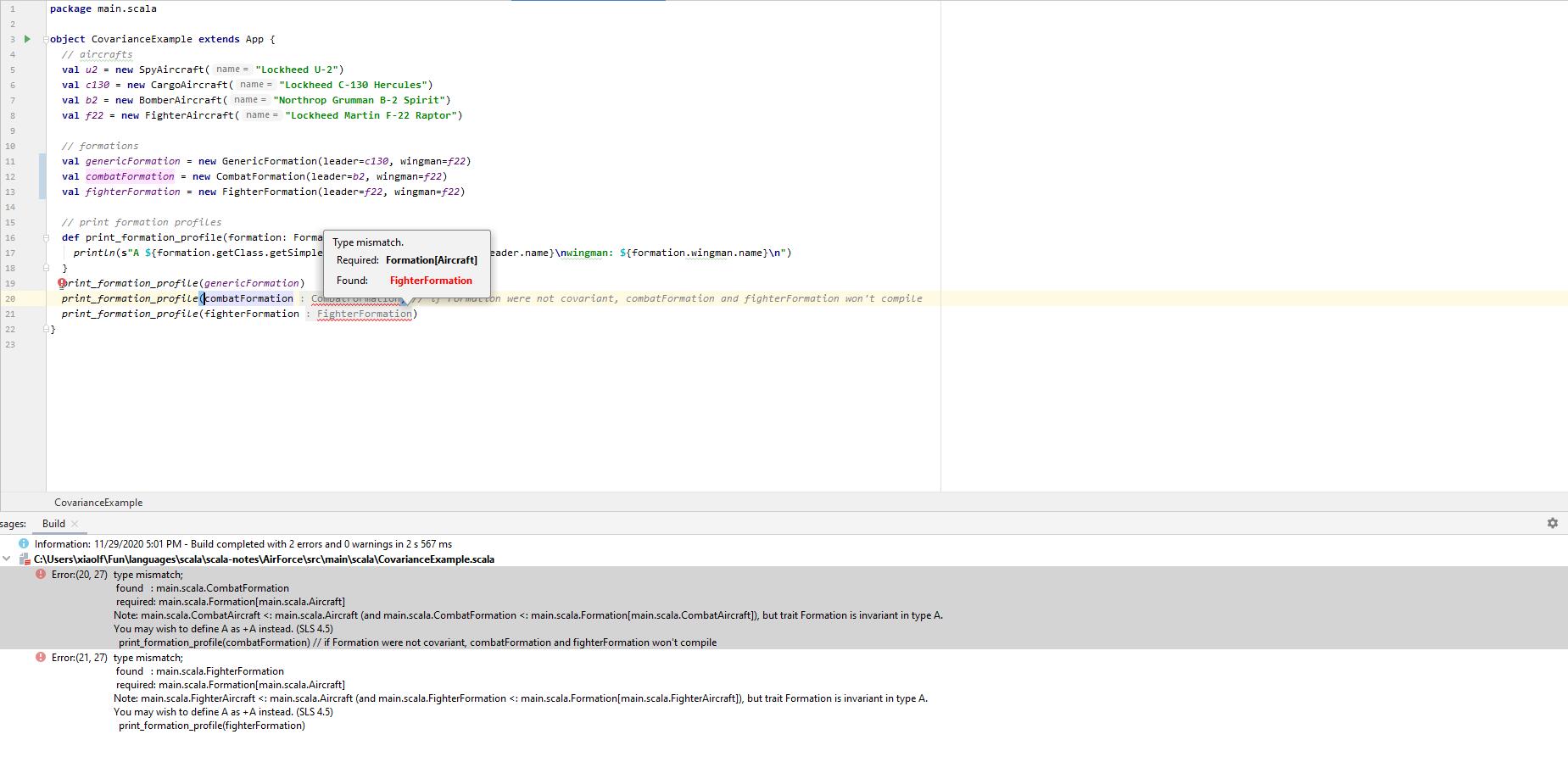
  print_formation_profile(combatFormation) // if Formation were not covariant, combatFormation and fighterFormation won't compile
  print_formation_profile(fighterFormation)
}

We see that print_formation_profile is able to print the profile of all three types of formations. This is because Formation is covariant, and so all three formations are subtypes of Formation[Aircraft].

If Formation were to be invariant, the compiler would raise a type mismatch:

Contravariant Type: Pilot

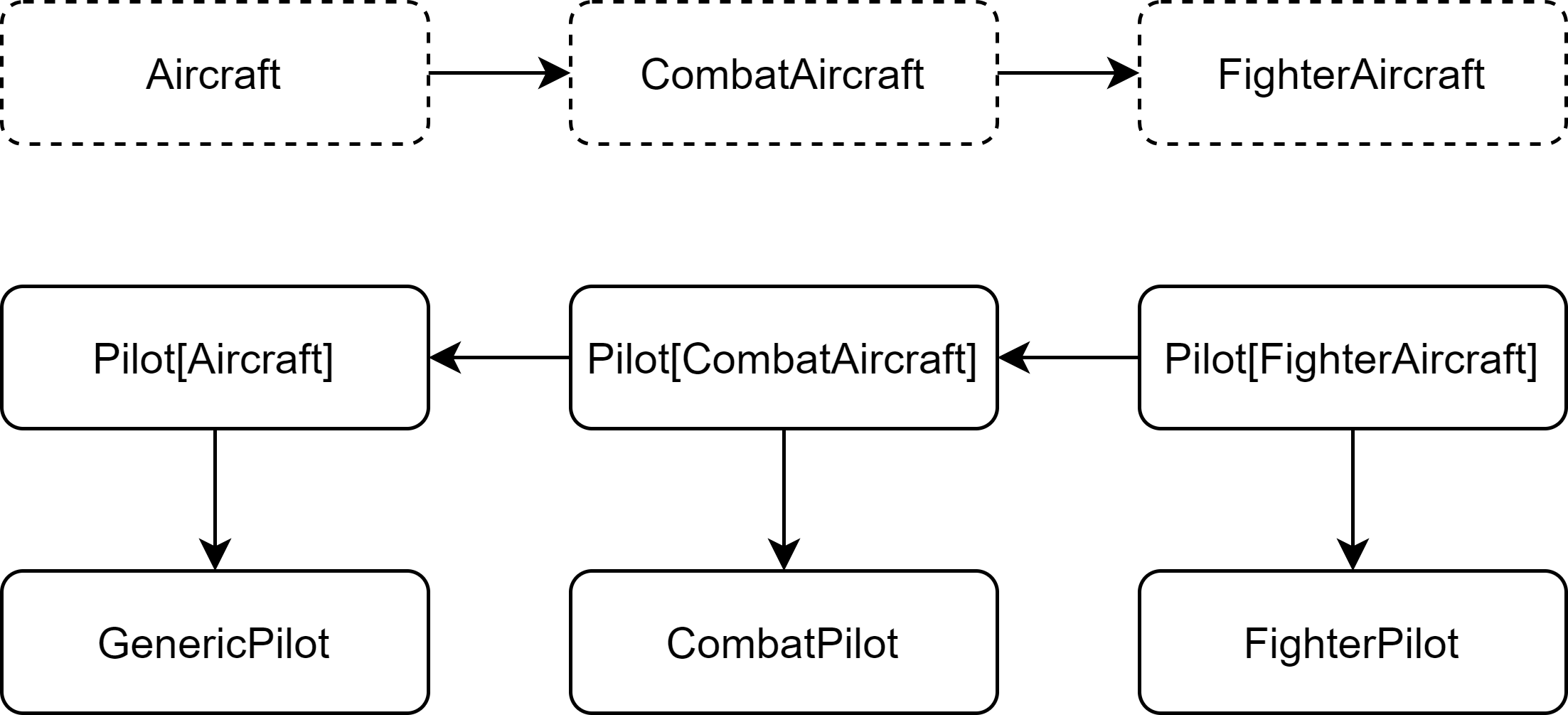
We define a contravariant type Pilot to fly the aircrafts.

trait Pilot[-A] { // contravariant in A
  def fly(aircraft: A): Unit
}

Then we define classes GenericPilot, CombatPilot, and FighterPilot that can fly any Aircraft, CombatAircraft, and FighterAircraft, respectively.

class GenericPilot() extends Pilot[Aircraft] {
  def fly(aircraft: Aircraft): Unit = {
    println(s"I'm a ${this.getClass.getSimpleName}, and I'm flying a ${aircraft.name} ${aircraft.getClass.getSimpleName}")
  }
}

class CombatPilot() extends Pilot[CombatAircraft] {
  def fly(aircraft: CombatAircraft): Unit = {
    println(s"I'm a ${this.getClass.getSimpleName}, and I'm flying a ${aircraft.name} ${aircraft.getClass.getSimpleName}")
  }
}

class FighterPilot() extends Pilot[FighterAircraft] {
  def fly(aircraft: FighterAircraft): Unit = {
    println(s"I'm a ${this.getClass.getSimpleName}, and I'm flying a ${aircraft.name} ${aircraft.getClass.getSimpleName}")
  }
}
Pilot is contravariant in Aircraft and it reverses the subtyping of Aircraft.

We define aircrafts, pilots, and fly methods that allow pilots to fly the aircrafts.

object ContravarianceExample extends App {
  // aircrafts
  val u2 = new SpyAircraft("Lockheed U-2")
  val b2 = new BomberAircraft("Northrop Grumman B-2 Spirit")
  val f22 = new FighterAircraft("Lockheed Martin F-22 Raptor")

  // pilots
  val genericPilot = new GenericPilot()
  val combatPilot = new CombatPilot()
  val fighterPilot = new FighterPilot()

  // fly methods
  def fly_generic(pilot: Pilot[Aircraft], aircraft: Aircraft): Unit = pilot.fly(aircraft)
  def fly_combat(pilot: Pilot[CombatAircraft], aircraft: CombatAircraft): Unit = pilot.fly(aircraft)
  def fly_fighter(pilot: Pilot[FighterAircraft], aircraft: FighterAircraft): Unit = pilot.fly(aircraft)

  // flying!
  fly_fighter(fighterPilot, f22)

  fly_combat(combatPilot, b2)
  fly_fighter(combatPilot, f22)

  fly_generic(genericPilot, u2)
  fly_combat(genericPilot, b2)
  fly_fighter(genericPilot, f22)
}

We see that genericPilot can fly all the aircrafts we defined via the respective fly method. This is because Pilot is contravariant, and so genericPilot is the most specific type among all the pilots we defined. As a result, it can be accepted as paramter by all the fly methods.

Similar Posts

prev Caching in Spark

next Spark Partitions

Content